C. Vilbrandt¹, G. Pasko², A. Pasko^2,3, P.-A. Fayolle¹, T. Vilbrandt¹, T. Kunii^2
1 University of Aizu, ² IT Institute, Kanazawa Institute of Technology, ³ Hosei University (Japan)

Abstract

We give an overview of existing digital data structures, the mathematical representation of objects, and the approaches to computer modeling of historical objects of cultural significance. Corresponding problems and solutions with long term archiving of digital data structures, constructive modeling, and a real time interactive display of the cultural heritage objects are discussed, various examples and applications are given.

Keywords: Cultural Heritage, Digital Preservation, Constructive Modeling, CSG, Function Representation, Fitting, Virtual Worlds

1. introduction

The digital preservation of cultural heritage objects through the use of digital constructive shape modeling is discussed in this paper. By digital preservation, we mean not only the digital reproduction of the surface shapes and colors of existing objects and the digital reconstructive modeling of objects that have already been lost, but also the digital representation and archiving of all of the physical properties of a cultural object or site, thereby allowing for the conservation of objects and accurate physical reconstruction of artifacts, which can be lost due to unexpected events. This is a particularly important issue in the realm of cultural heritage, since objects may be easily demolished, as the recent destruction of the Buddha images in Afghanistan has powerfully demonstrated.

Digital modeling and simulation technologies offer alternatives to textual and 2D image ontologies for cultural heritage objects and sites. However, this approach often relies on hardware and on proprietary software packages that may conceivably become obsolete and unusable even before the modeled objects themselves are destroyed. Accordingly, we propose and demonstrate a new mathematically based paradigm which avoids such pitfalls; that is Function Representation (FRep) based modeling using the HyperFun open source language. Some advantages of this approach are:

• The labor-intensive nature in measuring control points and fitting model parameters for modeling specific shapes can be alleviated with semi-automatic methods based on using 3D scanned points and control points and non-linear optimization for automatic fitting of parameters.

• The representation of three-dimensional surface microstructure (bumps, cracks, roughness) is possible to model with FRep as well as the simulation of the effects of aging or the effects of a particular artist''s technique, for example.

• Perhaps the most important advantage of the FRep geometric protocol is its open and simple textual format, making it highly suitable for long term digital data preservation and for the exchange of models among systems and people.

Constructive Solid Geometry (CSG) and Function Representation (FRep) are examined and practically applied as mathematical representations, which fit the purposes of long-term digital preservation. The importance of open-source methods for digital preservation is also discussed. Examples, including complex model data and resulting visualizations, of CSG based reconstruction of ancient Japanese temples and FRep based modeling of traditional Japanese lacquer ware are given.

In closing, practical issues concerning the implementation of a digital preservation system for cultural heritage objects are briefly outlined and discussed as the subject of future work.

2. DIGITAL PERSISTENCE AND PRESERVATION

First, we discuss the issues concerning the persistence of digital data structures and the need for long term digital preservation of cultural heritage objects. Preservation of cultural heritage objects with digital processes is not only theoretically possible but highly desirable for the reasons reviewed below. We raise with diligence two problems critical to the implementation of digital archiving technologies. Then, we proceed to discuss applications of digital representation, modeling, and simulation technologies needed for digital preservation including real-time interactive access to cultural heritage objects for educational and artistic environments.

1. Since each digital reproduction copy is a perfect copy, digital reproduction has the potential to allow archiving of data into the distant future.

2. In very small amounts of space, large amounts of data can be stored, making it feasible to have many copies in many locations, thus assuring against loss due to unforeseen events.

3. Much historical data and many cultural objects can not be accessed publicly (because of the cost and overhead of display, exotic locations, etc.), whereas digital data can be publicly accessed on demand globally.

4. Transparent learning through constant interaction with cultural objects in real time simulations, both locally and globally, is perhaps one of the most promising benefits from evolving digital modeling technologies.

5. Exponential evolutionary advancements of digital computational technologies will continue to provide more computational power and storage for less cost and space.

Digital archiving offers many benefits and has great promise, however there are several significant problems and possible solutions, which are discussed below.

Problem: Currently, digital data structures are dependent on the hardware, operating system, and hundreds of copyrighted or patented application processes that involve a multitude of companies. Digital data dependencies are a great problem. Because of the exponential evolutionary advancements of digital computational technologies mentioned above, most hardware and software is updated every year. Over three years, the changes are significant, and after six or seven years, the original data can not be accessed.

Solution: Develop digital data structures that are robust and independent of hardware, OS, and application modifications.

Problem: The source code for most current digital processes is not open for public inspection. This means that not only the processes are not verifiable, but, without access to the source code of the processes, the data which is dependent on the processes will die. Processes and data can not be migrated into the future.

Solution: The source code for all of the processes must be open for public inspection, modification and testing, and transparency of all operations. This assures the accuracy of the verification of the data, at the same time allowing for migration into the future. Transparency of complex digital manipulations entrusted with the long term digital preservation of cultural heritage is an essential key element to the development and implementation of a digital preservation system.

3. CONSTRUCTIVE MODELING / ENGINEERING

We are proposing a paradigm yielding more than visible surface models for display. The basic mathematical shape representation in digital preservation should serve several purposes. It should reflect the logic of the object's construction, support modeling of parametric families of shapes, support specific and extensible modeling operations, generation of polygonal and other surface models, as well as voxelization, and serve for direct control of rapid prototyping machines with the precision needed to reproduce the modeled objects. Our approach is based on constructive modeling that reflects the shapes, logical structure, and physical properties of materials and processes for the cultural object or site.

Constructive Solid Geometry (CSG) [9] and Function Representation (FRep) [15] are practically applied as mathematical representations of the structure engineering at the same time providing for the independent robust data structures necessary for the digital archiving of cultural heritage objects and sites. Using CSG, one can begin by selecting simple shapes (primitives), specifying their parameters and positions in space, and then using them to construct more complex shapes by applying different set-theoretic operations. FRep is a generalization of traditional implicit surfaces, CSG, and other shape models. It represents an object by a continuous function of three variables as F(x,y,z)  0. The function can be easily parameterized to support modeling of a parametric family. In FRep, an object is represented by a tree structure similar to one used in CSG, reflecting the logical structure of the object construction, where leaves are primitives and nodes are operations. Recently, a more general “constructive hypervolume” model has been introduced [16], which allows for modeling multidimensional point sets with attributes, where an attribute is a mathematical model of an object property of an arbitrary nature (material, photometric, physical etc.). HyperFun [1] is a minimalist programming language supporting all notions of FRep and constructive hypervolume modeling. In this paper, we present a number of cultural heritage-related works which have been done in the framework of the HyperFun, an international free software project on functionally-based shape modeling, visualization and animation (www.hyperfun.org). Members of the HyperFun team, a freely associated group of researchers and students from different countries, have contributed to projects described in this paper.

Examples of independent CSG based reconstruction of historical temples and FRep based modeling of traditional Japanese lacquer ware and modern Russian sculptures are given. We also recognize the cost problems associated with large amounts of labor in the reverse construction (reverse engineering through constructive modeling) of cultural heritage objects. Accordingly, we are seeking ways to reduce the amount of time and skill to make constructive engineering details. Therefore, we examine the application of fitting of a parameterized FRep model from a cloud of data points as a step towards automation.

4. CSG Modeling and virtual heritage: Japanese temples

Unfortunately, computer-aided two-dimensional drafting remains common practice in architectural and mechanical design. The benefits of using three-dimensional graphics techniques in constructing models are obvious. First of all, models can be manipulated to provide multiple viewpoints. Rotating a model can provide a better understanding of the physical relationships of the components of the actual structure, as well as the construction techniques involved. Moreover, three-dimensional models can replicate the actual construction of the building itself, including features normally hidden to the eye, such as interior bracketing, and the model can be deconstructed to reveal such hidden features. The description of our work below on the two Buddhist temple buildings in the Aizu region of Japan illustrates these benefits.

1. Constructive modeling of historical buildings

Considering the authors' experience in lost work and data due to obsolescence of software and hardware, the authors specified CSG representation as the most promising persistent data structure for modeling historical architecture of the Aizu History Project [3]. All parts of two Japanese historical buildings, the Golden Hall at Enichiji and Sazaedô featured in this paper (Figs. 1, 4), were created whenever possible with only CSG based entities. However, because CSG is limited in its range of shape representation and the overall size of each model was extremely large, the thatch roof of the Golden Hall and the double helix ramp inside Sazaedô had to be represented by a polygonal mesh. We used AutoCAD rel 12 software with Advanced Modeling Extensions (AME). AME is the implementation of CSG with the CSG tree history. Furthermore AutoCAD rel 12 using AutoLISP allows for direct access to the CSG tree history and the creation of third party programs such as the creation of export programs for CSG data. The authors are creating a free source code HyperFun modeling module for AutoCAD rel 12. We have found many errors in the AutoCAD AME implementation of CSG. However, we only have access to the AutoCAD CSG data tree and not the source code for the AME CSG module.

The original modeling of Enichiji and Sazaedô began eight years ago on 386 and 486 Intel class machines using AME CSG. The computational demands using CSG representation were so high that sections of a single model had to be developed in many separate files on as many as four different machines. However, the authors knew that the exponential computational evolution would continue and, in a few years, we would be able to use one machine. There were significant problems in data creation and manipulation of sections of the buildings across separate files on different computers as the coordination was all manually done. When combining the files into one file, it is needless to say that this data overwhelmed even the fastest single system at that time. Now, the entire model of Sazaedô with polygon reduction can be handled easily in real time on current animation and rendering systems.

However, we have found errors in AME, such as the order of subtraction and union operations are not interchangeable in some cases and extrusion with taper is not accurate. Therefore, the quality of the AME CSG modeling database is in question. It will take more effort to extract the CSG data structure embedded in AME than it would to model the buildings again, but this is a part of our planned research. Since we started, the HyperFun modeling language based on function representation has been developed. The next step in our digital preservation research is the creation of a "CAD" style third party program for HyperFun in AutoCAD rel 12. This is the first step in developing a separate Synthetic CAD modeling system.

2. Golden Hall at Enichiji

The first structure that we modeled using the AutoCAD AME CSG system was the Golden Hall at Enichiji, a temple located at the foot of Mt. Bandai. Although Enichiji was the religious center of the region throughout much of the Heian period (794-1185), no buildings or images from that period are extant today. In order to produce a model of the Heian Golden Hall, the structure that housed the temple's most important Buddha-images, the authors relied on data introduced in archaeological site reports [4].

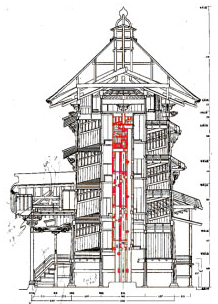
The construction of the Golden Hall model was a difficult task. At present the only solid information is the existence of seven foundation stones for pillars, demarking the north and part of the east walls. We have constructed the Golden Hall model (Fig. 1) using on-site measurements and some additional information.

In addition to archaeological data, the model was based on standard temple-building practices of the eighth and ninth centuries [5]. We also took into consideration the snowy climate of the Aizu region, which dictated a steeper roof slope than is common in other areas of Japan. In addition, we consulted Yamagishi Seiji, a master miya daiku (shrine carpenter) and the scion of an 800-year carpentry tradition in this region.

3. Sazaedô Pagoda

Recently declared a National Important Cultural Property, Sazaedô, a pagoda built in 1796 in Aizu-Wakamatsu, is noted for its unique architectural feature, a double-helical interior walkway. The double helical walkway is part of an interior tower (Fig. 2). (For more details on the Sazaedô construction, including black and white reproductions of these figures and some others, see [22]. The drawings in the figures below were adapted from engineering blueprints done in 1965 by Kobayashi Bunji.)

The 3D CAD model can be used to display all components separately, so that the construction may be seen and understood. Even an actual visit to the site does not enable such views. For example, the entrance and its canopy are structures which can be better understood from the model than from a photograph or even from a visit to the actual site, since they are complex objects and access and sightlines are restricted [23].

Figure 2: Interior tower colorized showing alcoves, drawing
    showing  the location of the interior tower.

By using measurements from an engineering drawing (Fig. 3 upper left) of the roof, and supplementing them with measurements taken on site, a 3D CAD model was constructed, and is displayed in the rendered views (Fig. 4). It is possible to select only one section from the single CAD model of the entire structure, and display it from multiple viewpoints and with various levels of detail (Fig. 5). Because of the constructive approach, any part, such as the helical structure, may be rendered without displaying the other components (Fig. 6), and an external shell may be fully rendered (Figs. 7 and 9).

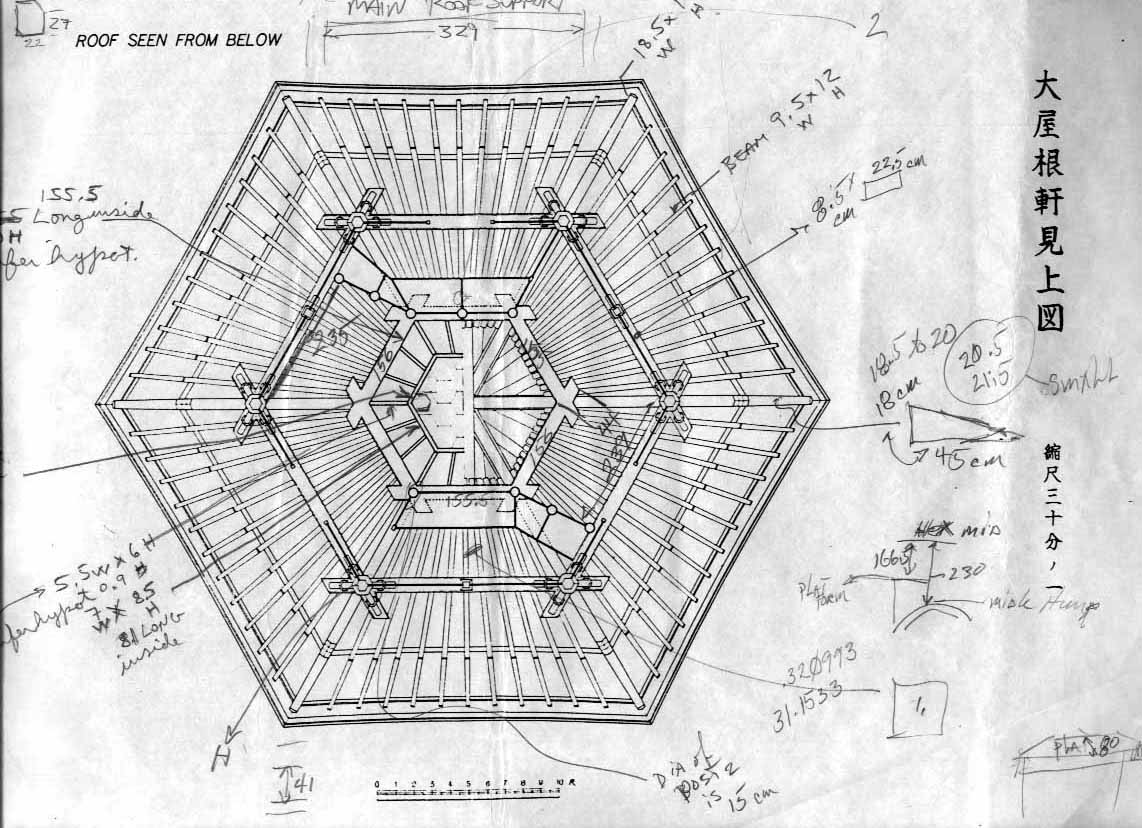
Figure 3: Engineering drawing of the roof.

Figure 4  - Sazaedô composite views: two roof views - outside shell and helic ramp, side and top views - inside core - outside porch. - entrance roof - full veiw from the front - see through construction views showing the helic ramp -  Two Virtual Reality (VR) views with texture mapping from an immersive enviroment useing a head mounted display.   in process -

Figure 5: Photo showing exterior detail.

The models illustrated are virtual constructions using virtual lumber cutting, positioning and joining according to the specifications of the miya daiku based on empirical knowledge of the past. By virtual lumber cutting, positioning and joining, we mean that we create each piece of the temple from virtual parts that represent the shape of each piece of lumber in the same order that would have been used by the miya daiku. The virtual lumber cutting, positioning and joining empirically show the value of digital preservation of cultural heritage using constructive modeling. The 3D model has recently been used to produce high quality renderings of the interior of Sazaedô, as would be seen by a person walking through the structure, and to produce QuickTime and AVI movies of the journey through the temple (see http://ggpl.org/saza2001). We plan to enhance the current model by including 3D reproductions of the images formerly enshrined in the building. We also intend to develop VR facilities to allow the examination of these images independently, and to allow the viewing of parts of the structure that cannot be accessed in the actual building.

4. Virtual surfaces to synthetic objects

The miya daiku or shrine carpenter uses parts of the tree or piece of timber in a specific place or way to create what the miya daiku understands as a "living" harmonious structure. A simple example of this specific use of timber by the miya daiku is the fabrication of the main columns of the temple, which are cut from trees growing on four sides of a mountain. The orientation of these trees to the earth and to each other on the mountain is maintained as the columns in the temple structure. With the use of the constructive hypervolume model [16], we can reach beyond the virtual surfaces of a wooden object. In the future, with records of weather and growth rings of trees, we can synthetically grow a tree using volume modeling and fabricate synthetic pieces of timber, using the same type of traditional miya daiku procedures, to create a synthetic representation of such ancient temple structures. Synthetic simulations of the miya daiku procedures in constructing traditional temples would not only archive the historical objects themselves but allow us a deeper understanding of the miya daiku craft.

5. Making history realtime - versus rendertime

In our research, we are exploring the use of optimized real time game engines as a method of viewing 3D content. These applications provide built in logic to handle basic world properties like gravity and collision detection. In addition, 3D games provide highly intuitive and efficient user interfaces, advanced network code for multi-user distributed environments, and an open coding environment allowing unlimited customization [24].

In real time simulation using gaming methods, a user can interact with the program, as well as with other users, in an immersive and entertaining environment. However, the restrictions imposed on a real time environment are significant. Even at relatively slow frame rate of ten frames per second (barely adequate for games), all computation for each frame must be finished within 100 milliseconds. Even on the most powerful gaming systems, this hardly allows for the level of complexity we might want in a historical simulation model. Such desired levels can be pre-calculated or calculated on demand by computational grids and presented as visualizations in various formats inside the real time game environment, transparent to the user.

Currently, at the University of Aizu Computer Arts Lab, we have modeled such a system using Quake [20] as the front end client and POV-Ray as the back end server. Our test case is a model of the Enichiji temple. In order to provide an immersive environment, we have created a model of this temple which runs in Quake, and allows the user to climb the stairs, inspect the internal architecture, and move under, over, through and around the temple in full real time. At any location in the Quake environment, the user may choose a detailed POV-Ray rendered visualization (Fig. 10).

Figure 10: Inside the Enichiji temple model: on the left are views of the real time Quake models in low detail; on the right are detailed raytracings delivered to the client in seconds after a view is selected.

Currently, we are working to incorporate the HyperFun geometric modeling language into the Quake game engine and Web technologies.

5. parameterized FRep modeling: lacquer ware

   1. FRep modeling of Japanese lacquer ware

We illustrate here the preservation of traditional crafts such as lacquer ware (Japanese shikki) manufacturing using FRep modeling. The “Virtual Shikki” project [18] includes the following activities:

• Reconstruction of shapes and making parametric families of models of representative shikki items. A parametric family of models allows us to generate samples of a specific model with different sizes, width/height ratios, and so on, without repeating the entire modeling process, and to apply parameters fitting from the real object measurements and scanning

• Digitizing textures. There are technical problems of scanning colored textures from the surface of existing lacquer ware items.

• Producing 3D virtual objects and presenting them on the Web. [25] using Virtual Reality Modeling Language (VRML) (see Fig. 11).

The process of modeling shikki shapes included selection of representative items, measurements of the coordinates of control points, introduction of the basic logical structure of the model (primitives and operations), description of the parameterized constructive model using the HyperFun language, visualization, and selection or fitting parameters of the model. Development of some additional specific operations, for example, bounded blending [17] were required for adequate modeling of shikki shapes.

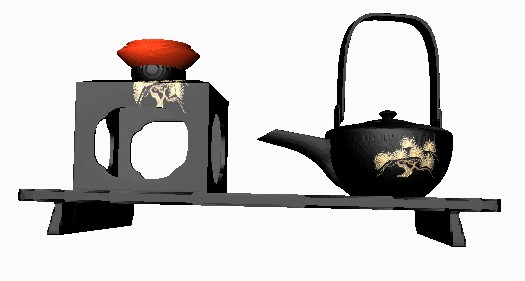
Figure 11: Front and top views of a Virtual Shikki object.

2. Fitting as an FRep modeling tool

Modeling specific shapes based on real world objects require a large amount of routine labor in measuring control points and fitting model parameters. Semi-automatic methods based on using 3D scanned points as control points and non-linear optimization for automatic fitting of parameters can be used to make the work of the modeler easier.

Some of the most useful methods for solving the problem of nonlinear optimization for fitting parameterized models in the least square sense are briefly discussed here and then applied to the concrete example of the sake pot presented above in the Virtual Shikki case study.

1. Nonlinear least square approach

Given a parameterized FRep model that describes the global shape of the object, and a set of 3D points on or near the surface of this object, the task is to recover the best set of parameters so that the parameterized FRep model closely fits the data points. The 3D points, typically obtained by a scanner, serve as control points for the final shape of the object. The vector of parameters from the FRep model control the final shape and the best fitted parameters should give the closest possible model according to the information provided by the control points.

For estimation of general distance of the point cloud to the surface with the current vector of parameters, a fitness function is needed. The FRep model itself can serve for defining such an algebraic distance. The least square error, or error of fit, for the model is the sum of the square of the defining function at all points. Techniques of function minimization can be used with the least square error function. FRep models are essentially nonlinear, and so is the least square error. Therefore, local and global nonlinear minimization techniques are considered below.

2. Local methods for nonlinear minimization

The most traditional methods for solving problems of nonlinear least square fitting are Levenberg-Marquardt or Newton type methods [6,14,19]. Such methods rely on a local quadratic approximation of the function being minimized; this quadratic approximation is obtained by a Taylor series expansion of the function in the vicinity of the current vector of parameters. The algorithms of Levenberg Marquardt and Newton methods search iteratively for a privileged direction to go in the parameter space and a step length in that direction based on the information given by the gradient and the Hessian matrix of the function. For some parameter spaces with multiple local minima, such methods are likely to be trapped into a local minimum. Good initial parameters are very important, because they determine to which minimum the algorithm may converge.

3. Global methods avoiding local minima

In contrary to local methods for nonlinear minimization, global methods are intended to find the best possible solution to the optimization problem. The choice of the starting point in parameter space should cause less problems for these methods. Simulated annealing is one of these methods, that received a lot of attention for solving optimization problems, both in discrete and continuous spaces [8,11,13]. When trying to minimize a function usually only downhill steps are accepted, but in simulated annealing uphill steps can be accepted with a probability, initially close to 1 and decreasing to 0 with the temperature of the system. Methods based on simulated annealing may be a good alternative to classical direct methods in global optimum search among many local optima, but they are facing some major problem of efficiency: the objective function needs to be sampled a huge number of times before reaching convergence.

4. Hybrid methods for nonlinear minimization

In order to overcome problems of both methods presented in the previous sections, a two stage algorithm of nonlinear FRep fitting is proposed. At the beginning, a global method like simulated

annealing is used to identify the vicinity of the global minimum, then a local, faster method, is applied, to extract the parameters that closely fit the 3D point set. Switching to a local method occurs when the error is below some threshold or when the parameterized model looks close enough to the data set. The result of this two stage process is a method faster than a pure global method, and it can also avoid the local minimum.

5. Experiments

The two stage process has been applied to the fitting of the parameterized FRep model of a sake pot in the Virtual Shikki project. The initial set of control points includes 27048 3D points on or near the surface of the object (see Fig. 12).

Figure 12: Point data set used for reverse construction (black) and an intermediate shape during the fitting process (green).

The parameterized FRep model has four free parameters meaning the position of the object in the space, the radius of the main body, and the last one controlling the shape of the handle.

It took 347 seconds on a Pentium IV processor laptop for the two stage algorithm to converge to the global minimum. Most of the time is spent in the global minimization procedure (341 seconds). Fig. 13 shows intermediate steps of the evolution of the shape during the fitting process.

Figure 13: Evolution of the shape of the sake pot
during the fitting process.

6. DIGITAL PRESERVATION IMPLEMENTATION

We are developing a set of robust CAD modeling tools based on the FRep / HyperFun language. Using the obsolete AutoCAD rel 12 /w AME we have created HyperFun models of box, cone,cylinder, and torus, demonstrating the ability to migrate our CSG models to HyperFun models.

One of our goals is to create a HyperFun module for AutoCAD rel 12 for preliminary testing of a HyperFun based CAD program. We intend to use a real time immersive interface for modeling (similar to that for public query illustrated in Section 4.5 above) such that the user using low resolution models can query and modify precise HyperFun models much in the same manner as an imprecise rasterized line is used in current CAD systems to visualize, query and modify precise CAD models.

The formation of the HyperFun NPO to coordinate research and development among a global network of researchers is a major and critical step in the implementation of a Digital Preservation System (DPS) which includes modeling and simulation tools for use by the cultural heritage community.

1. Digital Preservation System Scope

The intended scope of the DPS for cultural heritage objects may be defined as the mathematical modeling of any number of static or dynamic physical properties of an object or site, providing a common, independent abstract structure for synthetic modeling, visualization and simulation. Thus, the DPS could serve as a vehicle for analysis and data transport between current and future digital platforms for centuries to come, a necessary goal for digital archiving validity.

The DPS system would provide:

• Scientific definition of cultural heritage objects sufficient for available levels of detail for casual public browsing and on demand levels of detail and precision expected and required by academics, museum professionals and researchers in the field.

• Wide area information exchange, integration of heterogeneous sources and the curated knowledge of museums for other museums, universities and the general public abstracted from any specific local context.

• Immersive, synthetic, real-time simulations specifically intended to cover contextual information providing a transparent learning environment focused on: the historical, geographical and theoretical background in which individual cultural objects are placed, emphasizing their significance and value.

• Physical reconstruction or conservation of objects or sites lost due to unexpected events.

• Interoperability with metadata and legacy systems.

7. conclusion

We described an approach to digital shape preservation based on constructive shape modeling. We examined and selected Constructive Solid Geometry and Function Representation as shape representations that fit the purposes of long-term digital preservation. While this approach seems labor-intensive, it has several distinct advantages over methods based on automatic surface scanning and almost-automatic polygonal mesh generation. The purpose of a particular project should determine which method to use. If only visualization or animation from a distant viewpoint is needed, then polygonal mesh or other BRep models can be satisfactory. However, even a virtual walkthrough allowing close inspection of the object requires more accurate and detailed modeling. Constructive modeling helps to reveal knowledge about a shape's logical macrostructure. The representation of three-dimensional surface microstructure (bumps, cracks, roughness) is also out of the range of BRep abilities, but it is possible to model it using Frep. FRep's major disadvantage, its labor-intensive nature, can be reduced gradually by introducing semi-automatic methods based on 3D scanning of real objects with acquisition of control points and non-linear optimization for automatic fitting of the parameters of the constructive objects as we have illustrated in this paper.

Future work will include:

• Automation of the logical structure extraction.

• Creation of an interactive immersive modeling system (see [2,10] as examples).

• Investigation into linking the HyperFun language to metadata systems currently being developed and used by the cultural heritage community.

references

[1] V. Adzhiev, R. Cartwright, E. Fausett, A. Ossipov, A. Pasko, V. Savchenko, HyperFun project: a framework for collaborative multidimensional FRep modeling, Implicit Surfaces '99, Eurographics/ACM SIGGRAPH Workshop, J. Hughes and C. Schlick (Eds.), 1999, pp. 59-69, URL: http://www.hyperfun.org

[2] V. Adzhiev, P. Comninos, A. Pasko, Augmented sculpture: computer ghosts of physical artefacts, Leonardo, MIT, vol. 36, No. 3, 2003, pp. 211-219.

[3] Aizu History Project, URL:

http://www.cs.ucla.edu/~jmg/ah/menu.html

[4] Bandai Machi Kyoiku Iinkai (Ed. and Pub.), Shiseki Enichiji Ato IX, 1994.

[5] A. Brown, The Genius of Japanese Carpentry, Kodansha, 1989.

[6] J.E. Dennis, D.M. Gay, and R.E. Welsch, An adaptative nonlinear least-squares algorithm, ACM Transaction on Mathematical Software 7 (1981), 348-368.

[7] E. Fausett, A. Pasko, V. Adzhiev, Space-time and higher dimensional modeling for animation, Computer Animation 2000, IEEE Computer Society, 2000, pp.140-145.

[8] W. Goffe, G. Ferrier, and J. Rogers, Global optimization of statistical functions with simulated annealing, Journal of Econometric 60 (1994), 65-99.

[9] C. Hoffmann, Geometric and Solid Modeling, Morgan Kaufmann, 1989.

[10] M. Kazakov, V. Adzhiev, A. Pasko, Fast navigation through an FRep sculpture garden, Shape Modeling International 2001, IEEE Computer Society, 2001, pp.104-113.

[11] S. Kirkpatrick, C. Gelatt, and M. Vecchi, Optimization by simulated annealing, Science 220 (1983), 671.

[12] J. McCormac and A. Sherstyuk, Creating and rendering convolution surfaces, Computer Graphics Forum 17, No. 2, (1998),.pp. 113-120

[13] N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, and E. Teller, Equations of state calculations by fast computing machine, J. Chem. Phys. 21 (1953), 1097.

[14] J. More, The Levenberg-Marquardt algorithm implementation and theory, Lecture Notes in Mathematics No. 630 Numerical Analysis, vol. 630, New-York, 1978, pp. 105-116.

[15] A. Pasko, V. Adzhiev, A. Sourin, V. Savchenko, Function representation in geometric modeling: concepts, implementation and applications, The Visual Computer, vol.11, No.8, 1995, pp.429-446.

[16]. A. Pasko, V. Adzhiev, B. Schmitt, C. Schlick, Constructive hypervolume modeling, Graphical Models, vol. 63, No. 6, 2001, pp. 413-442.

[17] G. Pasko, A. Pasko, M. Ikeda, T. Kunii, Bounded blending operations, Shape Modeling International 2002, IEEE Computer Society, 2002, pp. 95-103.

[18] G. Pasko, A. Pasko, C. Vilbrandt, and T. Ikedo. Virtual Shikki and Sazaedo: Shape modeling in digital preservation of Japanese lacquer ware and temples, Proceedings of the 17th Spring Conference on Computer Graphics, Editors R. Durikovic and S. Czanner, IEEE Computer Society, 147–154, 2001.

[19] W. Press, B. Flannery, S. Teukolsky, and W. Vatterling, Numerical Recipes in C - the Art of Scientific Computing, Cambridge University Press, Cambridge, 1992.

[20] Quake, ID Software, URL: http://www.idsoftware.com

[21] B. Schmitt, A. Pasko, V. Adzhiev, C. Schlick, Constructive texturing based on hypervolume modeling, Journal of Visualization and Computer Animation, vol. 12, No. 5, 2001, pp. 297-310.

[22] C. Vilbrandt, et al., Computer models of historical sites: Sazaedo – from the Aizu History Project, Proceedings, EBTI, ECAI, SEER & PNC Joint Meeting (Academia Sinica), 1999, pp. 489-502.

[23] C. Vilbrandt, A. Pasko, G. Pasko, J.M. Goodwin, and J. Goodwin, Digital preservation of cultural heritage through constructive modeling, International Cultural Heritage Informatics Meeting ichim01, D. Bearman and F. Garzotto (Eds.), Vol. 1, 2001, pp. 183-200.

[24] T. Vilbrandt, C. Vilbrandt, C. Calef, J.R. Goodwin, J.M. Goodwin, Making it realtime: exploring the use of optimized realtime environments for historical simulation and education, Museums and the Web 2002: Selected Papers, Archives & Museum Informatics, D. Bearman and J. Trant (Eds.), Boston, 2002. URL:
http://www.archimuse.com/mw2002/papers/calef/calef.html

[25] Virtual Shikki, URL:
http://www.k.hosei.ac.jp/ ~pasko/Shikki/Shikki.html