 |
 |
Carl Vilbrandt (a),
Alexander Pasko (b), Galina Pasko (c,a),
Janet R. Goodwin
(d),
James M. Goodwin (e),
and Tosiyasu L. Kunii
(c,a)
(a) University of Aizu, Computer
Arts Lab, Aizu-Wakamatsu, Japan
E-mail: vilb@u-aizu.ac.jp
(b) Hosei University, Department
of Digital Media, Tokyo, Japan
E-mail: {pasko,kunii}@k.hosei.ac.jp
(c) IT Institute of Kanazawa
Institute of Technology, Tokyo, Japan
E-mail: gpasko@iti.kanazawa-it.ac.jp
(d) Director of the
Aizu History Project, Los Angeles (CA), USA
E-mail: jan@pollux.csustan.edu
(e) University of California
Los Angeles, Department of Computer Science, Los Angeles (CA), USA
E-mail: jmg@cs.ucla.edu
.ABSTRACT The issues of digital preservation of shapes and internal structures of historical and cultural objects are discussed. An overview of existing approaches to computer modeling of shapes is presented and corresponding problems are considered. We propose a digital preservation paradigm quite different from the currently popular "scan and mesh" approach yielding visible surface models. Our approach is based on constructive modeling that reflects the logical structure of modeled shapes. Constructive Solid Geometry (CSG) and Function Representation (FRep) are examined and practically applied as mathematical representations, which fit the purposes of long-term digital preservation. The importance of open-source methods for digital preservation is also discussed. Examples of CSG based reconstruction of historical temples and FRep based modeling of traditional lacquer ware are given.
KEYWORDS: constructive solid geometry, cultural heritage, digital preservation, function representation.
This paper will discuss the preservation
of cultural heritage objects through the use of computer techniques.
By preservation we mean not only the digital capture of existing objects
and the reproduction of objects that have already been lost, but also the
archiving of digital data into the foreseeable future. This is a
particularly important issue in the realm of cultural heritage, since objects
may be easily demolished, as the recent destruction of the Buddha-images
in Afghanistan has powerfully demonstrated.
The preservation of cultural heritage
has attracted considerable attention in computer graphics, geometric modeling,
and virtual reality communities.1 In this paper, we demonstrate
two methods of modeling cultural heritage objects. Our first method,
which we have used to model buildings from both archaeological data and
on-site measurements, reveals how the actual objects were constructed,
rather than yielding only the visible surface models produced by the currently
popular "scan and mesh" approach. Like most current methods of modeling,
however, this approach relies on hardware and on proprietary software packages
that may conceivably become obsolete and unusable even before the modeled
objects themselves are destroyed. Accordingly, we next propose and demonstrate
a new mathematically based paradigm that avoids such pitfalls. Our paradigm
is based on constructive modeling, which reflects the logical structure
of the shapes reproduced. We illustrate this new method with models of
traditional Japanese lacquer ware.
Scientific and other academic study demands rigorous proof concerning the accuracy of data gathering methods, research procedures, and digital processes that are used in a given project. These methods and procedures must be open to inspection and inquiry, and verifiable independent evaluation of the results of a given study should be performed if possible. Moreover, information must be disseminated and archived using an open and understandable data format and a stable storage medium that provides secure storage and retrieval, at a reasonable cost, for the near and distant future. Most digital information technology presently used in scientific and other academic studies does not meet these basic requirements. This paper presents several views of this problem and suggests possible solutions. The body of the paper focuses on computer modeling issues of pivotal importance to the development and establishment of secure digital archives for cultural heritage preservation.
The following problems occur in some current computer modeling methods:
• Violation of well-established norms, such as the right hand rule with Z-axis up, is in conflict with scientific and engineering procedures.Problems with traditional methods are not limited to the five
• Data is not accurate enough to make models which are
consistent at every level of detail.
• Proprietary data formats embedded in operating systems and hardware platforms make it difficult and illegal to access the data directly, thus making it impossible to verify the application's operations independently and difficult to translate or provide interoperability or migration across platforms. This snarled and secretive situation limits the life of the data.
• Proprietary methods and processes make it impossible to know how a given process works, what is accomplished, and whether or not the results are reproducible. It is self evident that unknowable and unverifiable procedures are unacceptable for archiving data.
• Data structures resulting from mathematical procedures used in most modeling software today are not only proprietary, but also inaccurate and poorly-defined. Therefore, the data structure prevents migration to future hardware and software upgrades.
On the other hand, geometric digital
modeling procedures and the fundamental mathematical base for shape modeling,
volume rendering, and the mathematical modeling of multiple dimensions
embedded in 3D modeling procedures are not well known or understood in
the digital archiving community. These are core issues in the development
and establishment of digital archives. Basic geometric modeling procedures,
the retention of originating
data attached to these procedures,
and the retention of the order of constructive events and the modeling
and embedding of physical dynamic attributes of 3D models for the creation
of synthetic processes and simulations will change the way we look at digital
data.
Most of the digital computer modeling tools used for historical and archaeological research and visualization produce data sets based on closed and proprietary source processes and data formats that have extremely short lifetimes for reasons cited above, thus making them unsuitable for archival purposes. The de facto standard commercial CAD and animation products should be rejected by their proprietary nature alone as procedurally acceptable for scientific use. These de facto standard commercial products are restricted to the resources of a single computer using modeling procedures based on polygonal meshes and other boundary representations (see below) that have proven inadequate and inconsistent over the last twenty years. We are all intellectually impoverished, when commercial proprietary products and data formats are accepted and used in academic circles as de facto standard tools with little other choice. Below, we propose some methods to remedy this problem.
Boundary Representation and Constructive Solid Geometry
There are several different ways to represent solids digitally. Each representation has to provide determination of point membership: given any point it must be possible to determine whether it is inside, outside, or on the surface of a solid. In this section, we describe basic representational schemes: boundary representation and Constructive Solid Geometry. Formal definitions and more details on solids and solid representations can be found in [7, 10].
Boundary
Representation. A solid can be represented by its boundary.
To define a boundary surface one can introduce points (vertices), curves
(edges), and surface patches (faces), and stitch them together (Fig. 1
upper). This boundary representation (or BRep) has two parts (Fig. 1 lower):
topological information of the connectivity of vertices, edges, and faces,
and geometric information embedding these boundary elements in three-dimensional
space. Topological information specifies incidences and adjacencies of
boundary elements. Geometric information specifies coordinates of vertices
or the equations of the surfaces containing the faces. The boundary of
the solid is a two-dimensional manifold. Each point of the boundary has
a neighborhood with one-to-one correspondence to a disk in the plane.
 |
A polyhedral solid is bounded by a set of planar polygons such that each edge connects two vertices and is shared by exactly two faces, at least three edges meet at each vertex, and faces do not interpenetrate. A simple polygon can be deformed into a sphere. The BRep of a simple polyhedron satisfies Euler's formula:
V – E + F = 2,
where V is a number of vertices, E is a number of edges, and F is a number of faces. The BRep including faces with holes satisfies the generalized Euler's formula:
V – E + F – H = 2(C – G),
where H is a number of holes in the faces, C is a number of solid disjoint components, and G is a surface genus (for sphere G = 0, for torus G = 1). These rules can be used to verify validity of the obtained BRep models.
Local modifications of the boundary are performed using tweaking operations such as moving the vertex, edge, or face. Topological modifications are performed using Euler operators, which include adding and removing vertices, edges, and faces. These operators satisfy Euler's formula and thus ensure topological validity of the resulting solids.
From the practical modeling point of
view, wire frame or BRep is used for visualization of CSG or FRep defined
objects. Currently, most commercial modeling programs use BRep not
only for visualization but also for mathematical definition of objects.
Systems based on this approach are exceedingly complex and prone to error.
The objects made in this manner may be aptly described as polygons with
holes and should not be considered archival quality digital objects.
In the practice of modeling with these systems, wire frame is convenient
for finding the center of arcs and circles and thus indispensable to the
creation and editing of entities, and BRep is helpful during the creation
and editing of entities and necessary for rendering the entities. Hybrid
systems using BRep based interaction and visualization together with mathematically
rigorous representation are needed for quintessential digital modeling
of objects.
 |
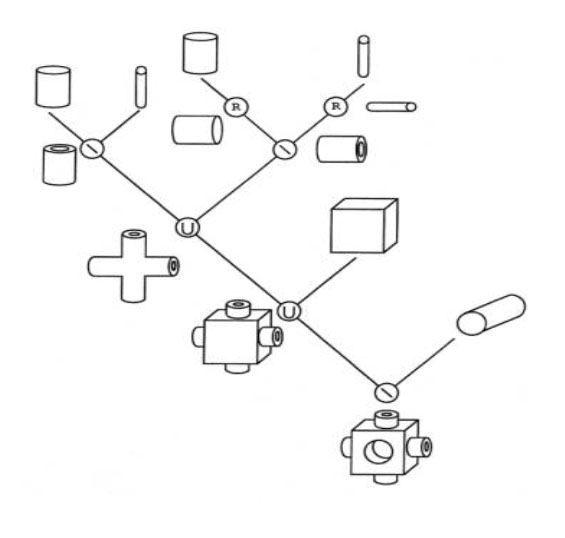
Using the modeling paradigm called Constructive Solid Geometry or CSG, one can begin by selecting simple shapes (primitives), specifying their parameters and positions in space, and then using them to construct more complex shapes by applying union, intersection, or subtraction set operations (Fig. 2). Traditional CSG primitives are the block, the cylinder, the cone, the sphere, and the torus. Linear transformations (translation and rotation) can be used together with regularized set operations. A regularized set operation includes removing lower dimensional parts of the standard set operation result such as dangling surfaces, curves or points.
A CSG object is represented as a binary tree (or CSG tree) with operations at the internal nodes and primitives at the leaves (Fig. 3). The point membership classification algorithm defines whether a given point is inside, outside, or on the boundary of the solid. This algorithm recursively traverses the CSG tree starting from the root. In the nodes with linear transformations, the inverse of the transformation is applied to the current point coordinates. When the recursion reaches the leaves, the point is tested against the corresponding primitives. Then, the classification results are combined in the internal nodes with set-theoretic operations.
 |